数据结构与算法之美(笔记)

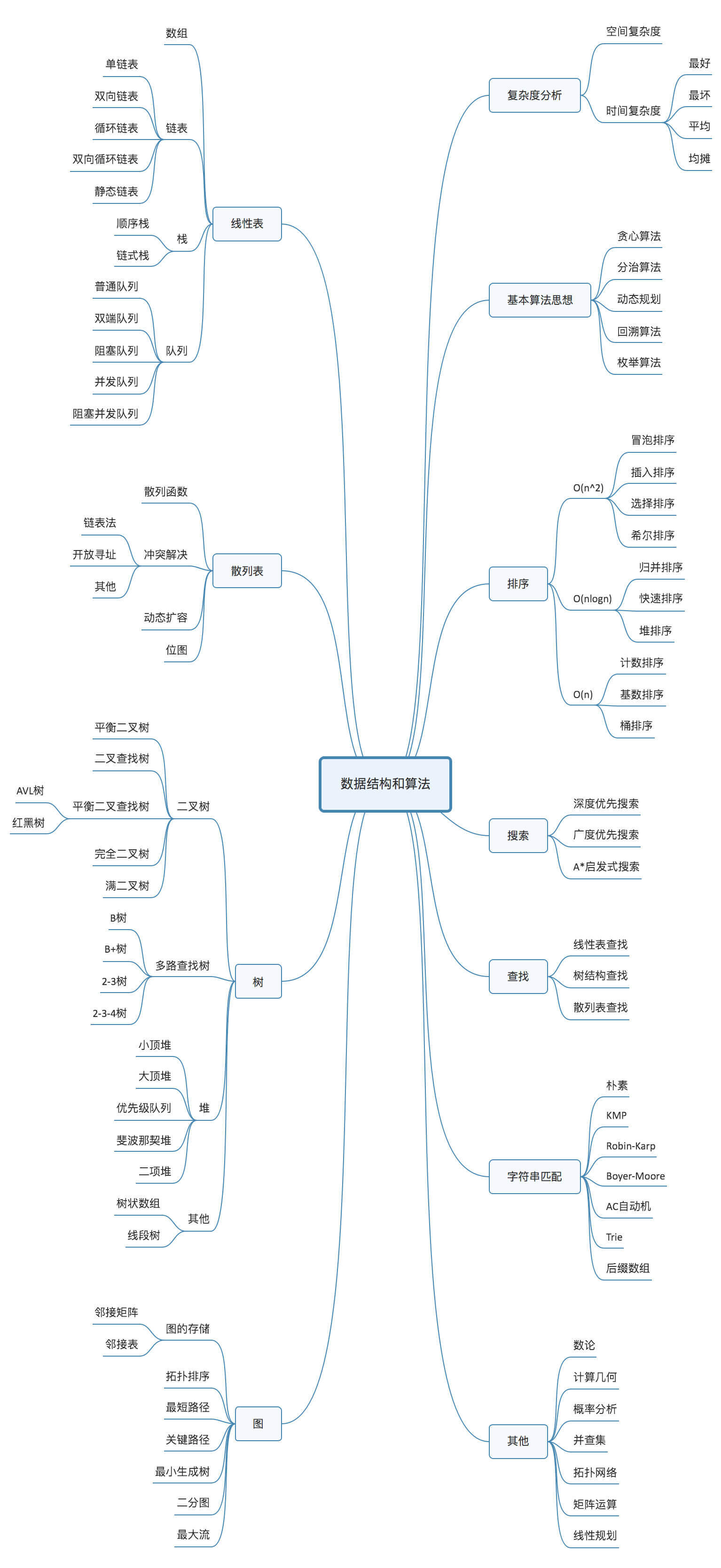
本文章为极客时间上王争老师的《数据结构与算法之美》学习笔记，图片截取自该专栏。

入门篇

01-为什么要学数据结构与算法？

目的:建立时间复杂度、空间复杂度意识，写出高质量的代码，能够设计基础架构，提升编程技能，训练逻辑思维，积攒人生经验。

02-如何抓住重点，系统高效的学习数据结构与算法？

什么是数据结构？什么是算法？

• 广义:数据结构就是指一组数据的存储结构，算法就是操作数据的一组算法。
• 狭义:指某些著名的数据结构与算法，比如队列、栈、堆、二分查找、动态规划等。

数据结构和算法的关系：

数据结构和算法是相辅相成的。数据结构是为算法服务的，算法要作用在特定的数据结构之上。

学习重点：

• 首先要掌握一个数据与算法中最重要的概念——复杂度分析

  数据结构和算法解决的是如何更省、更快地存储和处理数据的问题，因此，我们就需要一个考量效率和资源消耗的方法，这就是复杂度分析方法。

10个数据结构：数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie树。

10个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法。

一些事半功倍的学习技巧：

1. 边学边练，十度刷题。
2. 多问、多思考、多互动。
3. 打怪升级学习方法。
4. 知识需要沉淀，不要想视图一下子掌握所有。

03-复杂度分析（上）：如何分析、统计算法的执行效率和资源消耗？

复杂度分析是整个算法学习的精髓，只要掌握了他，数据结构与算法的内容基本上就掌握了一半。

为什么需要复杂度分析？

1. 测试结果非常依赖测试环境
2. 测试结果受到数据规模的影响很大

大O复杂度表示法

$T~(n)~ =O(f~(n)~)$

其中:$T~(n)$表示代码执行的时间；n表示数据规模的大小；$f(n)~$表示每行代码执行的次数总和。

大O时间复杂度实际上并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势，所以，也叫作渐进时间复杂度（asymptotic time complexity），简称时间复杂度。

例如：

1
2
3
4
5
6
7
8

int cal(int n) {
    int sum = 0;	1*unit_time
    int i = 1;		1*unit_time
    for( ; i <= n; ++i) {	n*unit_time
        sum = sum + i;		n*unit_time
    }
    return sum;
}

假设：每行代码执行的时间都是一样的，为一个单位时间（unit_time）。

即：$T~(n)~=(2n+2)*unit_time$

时间复杂度分析：

1. 只关注循环执行次数最多的一段代码。

   通常会忽略掉公式中的常量、低阶、系数，只需要记录一个最大阶的量级即可。

2. 加法法则：总复杂度等于量级最大的那段代码的复杂度。

3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。

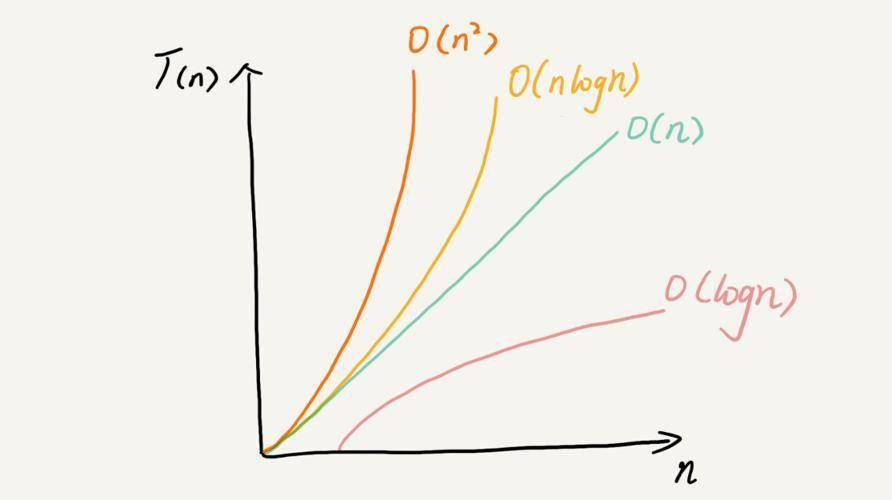
几种常见时间复杂度示例分析

把时间复杂度为非多项式量级的算法问题叫作NP（Non-Deterministic Polynomial，非确定多项式）问题。其中非多项式量级只有两个：$O(2^n)$和O(n!)。

1. O(1)

一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

2. O(logn)、O(nlogn)

在对数阶时间复杂度的表示方法里，我们忽略对数的“底”，统一表示为O(logn)。

如果一段代码的时间复杂度是O(logn)，我们循环执行n遍，时间复杂度就是O(nlogn)了。而且，O(nlogn)也是一种非常常见的算法时间复杂度。比如，归并排序、快速排序的时间复杂度都是O(nlogn)。

3. O(m+n)、O(m*n)

代码的复杂度有两个数据的规模来确定。

O(m+n)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

O(m*n)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

int cal(int m, int n) {
  int i = 1;
  int j = 1;
  int sum;
  for (; i < m; ++i) {
    for (; j < n; ++j) {
    	sum = sum + i*j;
  	}
  }
  return sum;
}

空间复杂度分析

空间复杂度全称就是渐进空间复杂度（asymptotic space complexity），表示算法的存储空间与数据规模之间的增长关系。

常见的空间复杂度就是O(1)、O(n)、$O(n^2)$，像O(logn)、O(nlogn)这样的对数阶复杂度平时都用不到。

04-复杂度分析（下）：浅析最好、最坏、平均、均摊时间复杂度？

最好情况时间复杂度（best case time complexity）、最坏情况时间复杂度（worst case time complexity）、平均情况时间复杂度（average case time complexity）、均摊时间复杂度（amortized time complexity）。

• 最好情况时间复杂度就是，在最理想的情况下，执行这段代码的时间复杂度。
• 最坏情况时间复杂度就是，在最糟糕的情况下，执行这段代码的时间复杂度。

基础篇

05-数组：为什么很多编程语言中数组都从0开始编号？

06-链表（上）：如何实现LRU缓存淘汰算法？

07-链表（下）：如何轻松写出正确的链表代码？

08-栈：如何实现浏览器的前进和后退功能？

09-队列：队列在线程池等有限资源池中的应用

10-递归：如何三行代码找到“最佳推荐人”？

11-排序（上）：为什么插入排序比冒泡排序更受欢迎？

12-排序（下）：如何使用快排思想在O~(n)~ 内查找第K大元素？

13-线性排序：如何根据年龄给100万用户数据排序？

14-排序优化：如何实现一个通用的、高性能的排序函数？

15-二分查找（上）：如何最省内存的方式实现快速查找功能？

16-二分查找（下）：如何快速定位IP对应的省份地址？

17-跳表：为什么Redis一定要用跳表来实现有序集合？

18-散列表（上）：Word文档中的单词拼写检查功能是如何实现的？

19-散列表（中）：如何打造一个工业级水平的散列表？

20-散列表（下）：为什么散列表和链表经常会一起使用？

21-哈希算法（上）：如何防止数据库中的用户信息被脱裤？

22-哈希算法（下）：哈希算法在分布式系统中有哪些应用？

23-二叉树基础（上）：什么样的二叉树适合用数组来存储？

24-二叉树基础（下）：有了如此高效的散列表，为什么还需要二叉树？

25-红黑树（上）：为什么工程中都用红黑树这种二叉树？

26-红黑树（下）：掌握这些技巧，你也可以实现一个红黑树？

27-递归树：如何借助树来求解递归算法的时间复杂度？

28-堆和堆排序：为什么说堆排序没有快速排序快？

29-堆的应用：如何快速获取到top10最热门的搜索关键字？

30-图的表示：如何存储微博、微信等社交平台网络中的好友关系？

31-深度和广度优先搜索：如何找出社交网络中的三度好友关系？

32-字符串匹配基础（上）：借助哈希算法实现高效字符串匹配？

33-字符串匹配基础（中）：如何实现文本编辑器中的查找功能？

34-字符串匹配基础（下）：如何借助BM算法轻松理解KMP算法？

35-Trie树：如何实现搜索引擎的搜索关键词提示功能？

36-AC自动机：如何用多模式串匹配实现敏感词过滤功能？

37-贪心算法：如何使用贪心算法实现Huffman压缩编码？

38-分治算法：谈一谈大规模计算框架MapReduce中的分治思想

39-回溯算法：从电影《蝴蝶效应》中学习回溯算法的核心思想

40-初识动态规划：如何巧妙解决“双十一”购物时的凑单问题？

41-动态规划理论：一篇文章带你彻底搞懂最优子结构，无后效性和重复子问题

42-动态规划实战：如何实现搜索引擎中的拼写纠错功能？

高级篇

43-拓扑排序：如何确定代码源文件的编译依赖关系？

44-最短路径：地图软件是如何计算出最优出行路径的？

45-位图：如何实现网页爬虫中的URL去重功能？

46-概率统计：如何利用朴素贝叶斯算法过滤垃圾短信？

47-向量空间：如何实现一个简单的音乐推荐系统？

48-B-树：MySQL数据库索引是如何实现的？

49-搜索：如何用A*搜索算法实现游戏中的寻路功能？

50-索引：如何在海量的数据中快速查找某个数据？

51-并行算法：如何利用并行处理提高算法的执行效率？

实战篇

52-算法实战（一）：剖析Redis常用数据类型对应的数据结构

53-算法实战（二）：剖析搜索引擎背后的经典数据结构和算法

54-算法实战（三）：剖析高性能队列Disruptor背后的数据结构和算法

55-算法实战（四）：剖析微服务接口鉴权限流背后的数据结构和算法

56-算法实战（五）：如何利用学过的数据结构和算法实现一个短网址系统？